푸아송 비

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

푸아송 비는 재료가 압축될 때 압축 방향에 수직인 방향으로 팽창하는 경향을 나타내는 지표이며, 늘어날 때는 늘어지는 방향에 수직인 방향으로 수축하는 경향을 나타낸다. 푸아송 비는 횡변형률을 종변형률로 나눈 값에 -1을 곱하여 계산하며, 대부분의 재료는 0에서 0.5 사이의 값을 갖는다. 재료의 기하학적 변화, 즉 길이 및 부피 변화를 통해 푸아송 비를 계산할 수 있으며, 등방성, 이방성, 직교 이방성, 횡등방성 재료 등 다양한 재료에서 푸아송 비의 특징이 나타난다. 일부 재료는 음의 푸아송 비를 보이기도 하며, 푸아송 효과는 가압 파이프 흐름, 구조 지질학, 코르크 마개, 자동차 정비 등 다양한 분야에서 응용된다.

더 읽어볼만한 페이지

재료역학 - 비등방성
비등방성은 재료의 미세구조, 결정구조, 분자 배열 등으로 인해 물질의 물리적, 화학적 성질이 방향에 따라 달라지는 현상으로, 다양한 분야에서 중요한 역할을 하며 측정 및 분석을 통해 재료 설계 및 응용에 활용된다.
재료역학 - 비틀림
비틀림은 물체에 동일하고 반대 방향의 힘이 작용하여 꼬이는 현상으로, 구조 부재에 비틀림 모멘트가 작용할 때 발생하며, 전단 응력을 유발하고, 비틀림 상수, 전단 응력, 비틀림 각도 등으로 분석되며 샤프트 설계에 중요하다.
구조역학 - 가상일
가상일은 역학계에서 외력이 가상 변위에 대해 하는 일의 합으로, 정역학에서는 계의 정적 평형 조건으로 활용되며, 달랑베르 원리를 통해 동역학에도 적용되어 구조 해석 및 계산에 널리 쓰이는 물리량이다.
구조역학 - 거더
교량 건설에 사용되는 구조 부재인 거더는 하중을 지지하며, 시공 방식과 형태에 따라 다양하게 제작된다.
연속체역학 - 온도
온도는 물체의 뜨겁고 차가운 정도를 나타내는 물리량으로, 열역학적으로는 에너지 이동 방향으로 정의되며, 미시적으로는 분자 운동 에너지의 평균값으로 정의되고, 화학 반응 속도와 생명체에 큰 영향을 미친다.
연속체역학 - 밀도
밀도는 단위 부피당 질량을 나타내는 물리량으로 질량을 부피로 나눈 값으로 계산되며, 온도와 압력에 따라 변하고, 진밀도, 겉보기밀도, 부피밀도, 탭밀도 등 여러 종류가 있고, 고대 그리스 시대부터 발전해왔다.

푸아송 비
개요
종류	탄성 계수
기호	ν
정의	가로 변형률 / 세로 변형률
SI 단위	무차원
차원	1
설명
푸아송 비	재료가 하중을 받을 때, 하중 방향의 변형률에 대한 수직 방향의 변형률의 비율
일반적인 값 범위	-1.0에서 0.5 사이
대부분의 재료	0.0에서 0.5 사이의 양수 값
특정 폼(foam) 재료	음의 푸아송 비를 가짐
팽창 재료	0.5의 푸아송 비를 가짐
등방성 재료	E = 2G(1 + ν) https://en.wikipedia.org/wiki/Poisson's_ratio#cite_note-3] E = 3K(1 − 2ν) https://en.wikipedia.org/wiki/Poisson's_ratio#cite_note-4] # - th: # td: # E = 2G(1 + ν) https://en.wikipedia.org/wiki/Poisson's_ratio#cite_note-3] # - th: # td: # E = 3K(1 − 2ν) https://en.wikipedia.org/wiki/Poisson's_ratio#cite_note-4]
여기서	E는 영률 G는 전단 탄성 계수 K는 체적 탄성 계수 # - th: # td: E는 영률 # - th: # td: G는 전단 탄성 계수 # - th: # td: K는 체적 탄성 계수
최대 푸아송 비	이론적 최대값: 0.5 대부분의 재료: 이 값에 미치지 못함
코르크	0에 가까운 값
고무	0.5에 가까운 값
음의 푸아송 비	특정 재료에서 관찰됨
오 auxetics	음의 푸아송 비를 갖는 재료
적용 분야	재료 과학 공학 지진학
관련 개념	탄성 계수 후크의 법칙 변형률 응력

2. 정의

푸아송 비는 재료가 한 방향으로 힘을 받을 때, 힘의 방향과 수직인 방향으로 발생하는 변형의 비율을 나타낸다. 이는 재료가 압축될 때 힘의 방향과 수직으로 팽창하는 푸아송 효과를 측정하는 지표이다.^[2] 고무 밴드를 늘리면 얇아지는 현상이 그 예시이다.

안정적이고, 등방성이며, 선형 탄성을 가지는 재료의 푸아송 비는 영률, 전단 탄성 계수, 체적 탄성 계수가 양수여야 한다는 조건 때문에 -1.0에서 +0.5 사이의 값을 가진다.^[3] 대부분의 재료는 0.0에서 0.5 사이의 푸아송 비 값을 갖는다.

강철과 단단한 폴리머는 설계 한계 내에서 사용될 때(항복 전) 약 0.3의 값을 가지며, 항복 후 변형의 경우 0.5까지 증가한다.^[4]
고무는 거의 0.5이다.
코르크는 0에 가깝다.
유리는 0.18에서 0.30 사이이다.
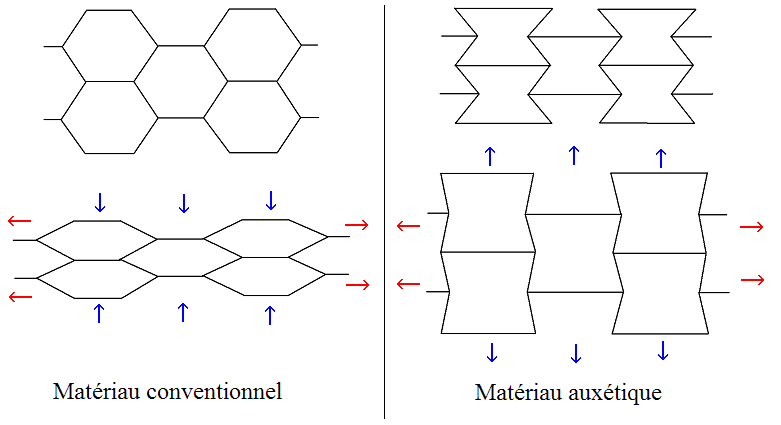
일부 폴리머 폼, 종이 접기,^[5]^[6] 및 특정 세포는 음의 푸아송 비를 나타낼 수 있으며, 오세틱 재료라고 한다.
탄소 나노 튜브, 지그재그 기반 접힌 시트 재료,^[7]^[8] 및 벌집형 오세틱 메타 물질^[9] 등 일부 이방성 재료는 특정 방향에서 0.5보다 큰 푸아송 비를 나타낼 수 있다.

2. 1. 푸아송 효과

재료가 압축되면 힘의 방향과 수직인 방향으로 팽창하고, 늘어나면 수축하는 현상을 푸아송 효과라고 한다.^[2] 예를 들어 고무 밴드를 늘리면 눈에 띄게 얇아진다. 어떤 물체에 ''z'' 축 방향으로 단축 응력(한 방향으로만 작용하는 응력)이 작용할 때, 물체의 탄성에 기초하여 ''z'' 축 방향의 치수가 늘어나 종변형률 ''ε_z''이 발생한다. 이때 부수적으로, ''z'' 축 직각 방향의 ''x'' 축과 ''y'' 축에도 횡변형률 ''ε_x''과 ''ε_y''가 발생한다.^[32]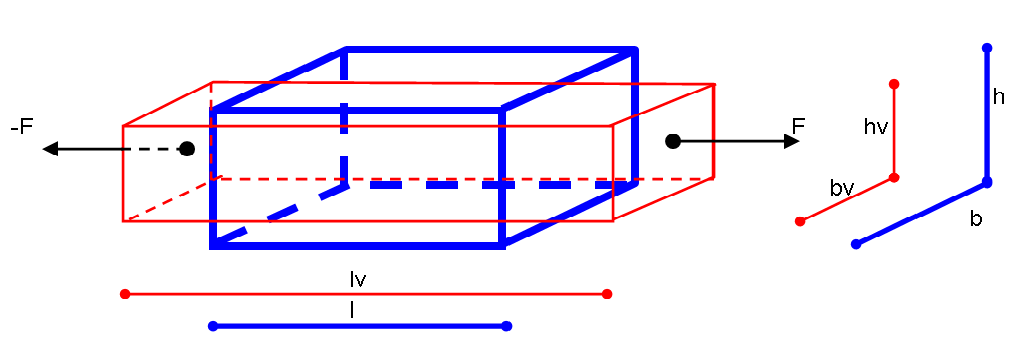

직육면체에 인장 하중이 가해질 때의 변형 모습
파란색이 하중 전 형태, 빨간색이 하중 후 형태

2. 2. 푸아송 비의 계산

푸아송 비(ν)는 가로 변형률(ε_trans)을 세로 변형률(ε_axial)로 나눈 후 음수 부호를 붙여 계산한다. 식으로 나타내면 다음과 같다.^[32]

:

\nu = -\frac{d\varepsilon_\mathrm{trans}}{d\varepsilon_\mathrm{axial}} = -\frac{d\varepsilon_\mathrm{y}}{d\varepsilon_\mathrm{x}}= -\frac{d\varepsilon_\mathrm{z}}{d\varepsilon_\mathrm{x}}

$\nu$ 는 푸아송 비,
$\varepsilon_\mathrm{trans}$ 는 가로 변형률,
$\varepsilon_\mathrm{axial}$ 는 축 변형률을 나타낸다.

어떤 물체에 ''z'' 축 방향으로 단축 응력(한 방향으로만 작용하는 응력)이 작용할 때, 물체의 탄성에 기초하여 ''z'' 축 방향의 치수가 늘어나 종변형률 ''ε_z''이 발생한다. 이때 부수적으로, ''z'' 축 직각 방향의 ''x'' 축과 ''y'' 축에도 횡변형률 ''ε_x''과 ''ε_y''가 발생한다. 이 현상을 '''푸아송 효과'''라고도 부른다.^[32]

이 횡변형률을 종변형률로 나누고, -1을 곱한 것이 푸아송 비 ''ν''이다.

:

\nu_x = -\frac{\varepsilon_x}{\varepsilon_z}, \nu_y = -\frac{\varepsilon_y}{\varepsilon_z}

방향에 관계없이 푸아송 비가 일정한 재료(등방성)의 경우에는 단순히 ''ν''로도 나타낸다.

:

\nu_x = \nu_y = \nu

푸아송 비의 역수를 '''푸아송 수'''라고 하며, ''m''으로 표시된다.^[31]

:

m = \frac{1}{\nu}

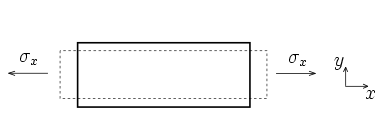
예를 들어, 가장 단순한 2차원 판에 한 방향으로만 응력 ''σ_x'' (단축 응력)이 가해지는 경우, 이 판 내의 응력과 변형률의 관계는 포아송 비 ''ν'' 와 탄성 계수 ''E'' 에 의해 다음과 같이 나타난다.^[31]

:

\begin{align}\varepsilon_{x} &= \frac{\sigma_x}{E}, \\\varepsilon_{y} &= -\frac{\nu \sigma_x}{E}\end{align}

위의 관계를 훅의 법칙이라고 부른다.

2. 3. 푸아송 수

어떤 물체에 ''z'' 축 방향으로 단축 응력(한 방향으로만 작용하는 응력)이 작용할 때, 물체의 탄성에 기초하여 ''z'' 축 방향의 치수가 늘어나 종변형률 ''ε_z''이 발생한다. 이때 부수적으로, ''z'' 축 직각 방향의 ''x'' 축과 ''y'' 축에도 횡변형률 ''ε_x''과 ''ε_y''가 발생한다. 이 현상을 '''푸아송 효과'''(Poisson effect)라고도 부른다.^[32]

이 횡변형률을 종변형률로 나누고, -1을 곱한 것이 푸아송 비 ''ν''이다.

:

\nu_x = -\frac{\varepsilon_x}{\varepsilon_z}, \nu_y = -\frac{\varepsilon_y}{\varepsilon_z}

방향에 관계없이 푸아송 비가 일정한 재료의 경우에는 단순히 ''ν''로도 나타낸다.

:

\nu_x = \nu_y = \nu

푸아송 비의 역수를 '''푸아송 수'''라고 하며, ''m''으로 표시된다.^[31]

:

m = \frac{1}{\nu}

3. 기하학적 변화로부터의 푸아송 비

'''그림 1''': 푸아송 비가 0.5인 등방성 선형 탄성 재료의 정육면체(길이 )가 x축 방향으로 인장력을 받을 때, 변형 전의 녹색 정육면체와 변형 후의 빨간색 정육면체를 비교하면, x축 방향으로 만큼 늘어나고 y축 및 z축 방향으로 만큼 줄어든 모습을 볼 수 있다.

x축 방향으로 늘어나는 정육면체의 경우(그림 1 참조), x축 방향으로 길이 증가(ΔL|Δ엘^영어)가 발생하고, y축 및 z축 방향으로 길이 감소(ΔL′|Δ엘 프라임^영어)가 발생한다. 이때, 무한소 대각 변형률은 다음과 같이 나타낼 수 있다.

:

d\varepsilon_x = \frac{dx}{x},\qquad d\varepsilon_y = \frac{dy}{y},\qquad d\varepsilon_z = \frac{dz}{z}.

푸아송 비가 변형되는 동안 일정하다면, 위 식을 적분하고 푸아송 비의 정의를 사용하면 다음과 같은 관계식을 얻을 수 있다.

:

-\nu \int_L^{L+\Delta L} \frac{dx}{x} = \int_L^{L+\Delta L'} \frac{dy}{y} = \int_L^{L+\Delta L'} \frac{dz}{z}.

이 식을 풀고 지수화하면 ΔL′|Δ엘 프라임^영어과 ΔL|Δ엘^영어 사이의 관계는 다음과 같이 표현된다.

:

\left(1+\frac{\Delta L}{L}\right)^{-\nu} = 1+\frac{\Delta L'}{L}.

ΔL|Δ엘^영어과 ΔL′|Δ엘 프라임^영어의 값이 매우 작을 경우, 1차 근사를 통해 다음과 같은 관계를 얻을 수 있다.

:

\nu \approx - \frac{\Delta L'}{\Delta L}.

재료가 늘어날 때 정육면체의 부피 변화를 상대적으로 계산하면 다음과 같다.

:

\frac{\Delta V}{V} = \left(1 + \frac{\Delta L}{L} \right)\left(1 + \frac{\Delta L'}{L} \right)^2 - 1

앞서 유도한 ΔL|Δ엘^영어과 ΔL′|Δ엘 프라임^영어 사이의 관계를 이용하면,

:

\frac {\Delta V} {V} = \left(1 + \frac{\Delta L}{L} \right)^{1 - 2\nu} - 1

ΔL|Δ엘^영어과 ΔL′|Δ엘 프라임^영어의 값이 매우 작을 경우, 1차 근사를 통해 다음을 얻는다.

:

\frac {\Delta V} {V} \approx (1-2\nu)\frac{\Delta L}{L}

등방성 재료의 경우, 라메의 관계식^[10]을 사용하여 푸아송 비를 다음과 같이 나타낼 수 있다.

:

\nu \approx \frac{1}{2} - \frac{E}{6K}

여기서 $K$는 체적 탄성 계수, $E$는 영률이다.

막대 형태의 재료에 장력이 가해져 길이가 ${\Delta L}$만큼 변하면, 지름(또는 너비, 두께) $d$는 다음과 같이 변한다.^[1]

:

\frac{\Delta d}{d} = -\nu \frac{\Delta L} L

위 공식은 작은 변형에만 적용된다. 변형이 큰 경우에는 다음 공식을 사용할 수 있다.^[1]

:

\Delta d = -d \left( 1 - {\left( 1 + \frac{\Delta L} L \right)}^{-\nu} \right)

$d$: 원래 지름
$\Delta d$: 지름 변화
$\nu$: 푸아송 비
$L$: 원래 길이
${\Delta L}$: 길이 변화

길이가 증가하면 지름은 감소하므로, $\Delta d$는 음수이다.^[1]

3. 1. 길이 변화

x 방향으로 늘어나는 정육면체의 경우(그림 1 참조), x 방향으로 길이 증가가 ΔL|Δ엘^영어이고, y 및 z 방향으로 길이 감소가 ΔL′|Δ엘 프라임^영어이면, 무한소 대각 변형률은 다음과 같다.

:

d\varepsilon_x = \frac{dx}{x},\qquad d\varepsilon_y = \frac{dy}{y},\qquad d\varepsilon_z = \frac{dz}{z}.

푸아송 비가 변형되는 동안 일정하다면, 위 식을 적분하고 푸아송 비의 정의를 사용하면 다음과 같다.

:

-\nu \int_L^{L+\Delta L} \frac{dx}{x} = \int_L^{L+\Delta L'} \frac{dy}{y} = \int_L^{L+\Delta L'} \frac{dz}{z}.

이를 풀고 지수화하면 ΔL′|Δ엘 프라임^영어과 ΔL|Δ엘^영어 사이의 관계는 다음과 같다.

:

\left(1+\frac{\Delta L}{L}\right)^{-\nu} = 1+\frac{\Delta L'}{L}.

ΔL|Δ엘^영어과 ΔL′|Δ엘 프라임^영어의 값이 매우 작을 경우, 1차 근사로 다음을 얻을 수 있다.

:

\nu \approx - \frac{\Delta L'}{\Delta L}.

3. 2. 부피 변화

재료가 늘어날 때 정육면체의 부피 변화를 상대적으로 계산하면 다음과 같다. 이므로,

:

V + \Delta V = (L + \Delta L)\left(L + \Delta L'\right)^2

위 식을 다음과 같이 유도할 수 있다.

:

\frac{\Delta V}{V} = \left(1 + \frac{\Delta L}{L} \right)\left(1 + \frac{\Delta L'}{L} \right)^2 - 1

앞서 유도한 과 사이의 관계를 이용하면,

:

\frac {\Delta V} {V} = \left(1 + \frac{\Delta L}{L} \right)^{1 - 2\nu} - 1

과 의 값이 매우 작을 경우, 1차 근사를 통해 다음을 얻는다.

:

\frac {\Delta V} {V} \approx (1-2\nu)\frac{\Delta L}{L}

등방성 재료의 경우, 라메의 관계식^[10]을 사용할 수 있다.

:

\nu \approx \frac{1}{2} - \frac{E}{6K}

여기서 는 체적 탄성 계수, 는 영률이다.

3. 3. 폭 변화

막대 형태의 재료에 장력이 가해져 길이가 ${\Delta L}$만큼 변하면, 지름(또는 너비, 두께) $d$는 다음과 같이 변한다.^[1]

:

\frac{\Delta d}{d} = -\nu \frac{\Delta L} L

위 공식은 작은 변형에만 적용된다. 변형이 큰 경우에는 다음 공식을 사용할 수 있다.^[1]

:

\Delta d = -d \left( 1 - {\left( 1 + \frac{\Delta L} L \right)}^{-\nu} \right)

$d$: 원래 지름
$\Delta d$: 지름 변화
$\nu$: 푸아송 비
$L$: 원래 길이
${\Delta L}$: 길이 변화

길이가 증가하면 지름은 감소하므로, $\Delta d$는 음수이다.^[1]

4. 특징적인 재료

일반적인 재료는 특정 방향으로 힘을 가하면 힘을 받는 방향뿐만 아니라 그와 수직인 방향으로도 변형이 일어난다. 이때, 재료에 따라 푸아송 비는 다른 값을 가진다.

대부분의 재료는 양의 푸아송 비를 가지지만, 특수한 구조를 가진 재료는 음의 푸아송 비를 가질 수 있다. 예를 들어, 실리콘 단결정, 크리스토발라이트(SiO₂로 이루어진 결정) 등은 음의 푸아송 비를 나타낸다. 펜타그래핀(오각형의 그래핀)^[33], 내부에 벌집 구조를 가진 재료^[34]도 방향에 따라 음의 푸아송 비를 나타낼 수 있다. 하지만 이러한 재료들은 모든 방향에서 같은 특성을 보이는 등방성 탄성체가 아니라, 방향에 따라 탄성 특성이 다른 이방성 재료이다.

재료의 특성에 따라 푸아송 비는 다음과 같이 분류할 수 있다.

등방성 재료: 재료의 모든 방향에서 탄성 특성(영률, 푸아송 비)이 동일하다. 등방성 재료의 푸아송 비 범위는 -1 < ''ν'' < 1/2 이다.
이방성 재료: 재료의 방향에 따라 탄성 특성이 다르다. 이방성 재료의 푸아송 비는 잡아당기는 방향과 가로 변형 방향에 따라 달라진다.
직교 이방성 재료: 서로 수직인 세 개의 대칭면을 가지는 재료로, 각 방향에 따라 다른 푸아송 비를 가진다. 예를 들어, 나무는 나뭇결 방향으로 가장 강하고 다른 방향으로는 약하다.^[13]^[14]
횡등방성 재료: 탄성 특성이 등방성인 평면을 가지는 재료이다.

4. 1. 등방성 재료

선형 등방성 재료가 압축력(수직력)만 받는 경우, 한 축 방향의 변형은 다른 축 방향으로 3차원의 변형을 일으킨다. 따라서 훅의 법칙을 3차원으로 일반화할 수 있다.^[31]

:

\begin{align}\varepsilon_{xx} &= \frac {1}{E} \left [ \sigma_{xx} - \nu \left ( \sigma_{yy} + \sigma_{zz} \right ) \right ] \\[6px]\varepsilon_{yy} &= \frac {1}{E} \left [ \sigma_{yy} - \nu \left ( \sigma_{zz} + \sigma_{xx} \right ) \right ] \\[6px]\varepsilon_{zz} &= \frac {1}{E} \left [ \sigma_{zz} - \nu \left ( \sigma_{xx} + \sigma_{yy} \right ) \right ]\end{align}

여기서:

, , 는 , , 방향의 변형률이다.
, , 는 , , 방향의 응력이다.
는 영률(등방성 재료의 모든 방향에서 동일)이다.
는 푸아송 비(등방성 재료의 모든 방향에서 동일)이다.

이 방정식들은 다음과 같이 표현할 수 있다.

:

\varepsilon_{ii} = \frac {1}{E} \left [ \sigma_{ii}(1+\nu) - \nu \sum_k \sigma_{kk} \right ]

일반적인 경우, 수직 응력뿐만 아니라 전단 응력도 존재하며, 훅의 법칙을 완전히 일반화하면 다음과 같다.

:

\varepsilon_{ij} = \frac {1}{E} \left [ \sigma_{ij}(1+\nu) - \nu \delta_{ij} \sum_k \sigma_{kk} \right ]

여기서 는 크로네커 델타이다. 아인슈타인 표기법을 사용하면,

:

\sigma_{kk} \equiv \sum_l \delta_{kl} \sigma_{kl}

이므로, 방정식을 다음과 같이 간단하게 나타낼 수 있다.

:

\varepsilon_{ij} = \frac {1}{E} \left [ \sigma_{ij}(1+\nu) - \nu \delta_{ij} \sigma_{kk} \right]

예를 들어, 2차원 판에 한 방향으로만 응력 ''σ_x'' (단축 응력)이 가해지는 경우, 판 내의 응력과 변형률의 관계는 푸아송 비 ''ν'' 와 탄성 계수 ''E'' 에 의해 다음과 같이 나타낼 수 있다.^[31]

:

\begin{align}\varepsilon_{x} &= \frac{\sigma_x}{E}, \\\varepsilon_{y} &= -\frac{\nu \sigma_x}{E}\end{align}

이 관계를 훅의 법칙이라고 부른다.

재료가 등방성 균질인 경우, 단위 체적당 변형 에너지인 '''변형 에너지 함수''' ''U''₀는 다음과 같이 나타낸다.^[31]

:

U_0 = \frac{E\nu}{2(1+\nu)(1-2\nu)}(\varepsilon_x + \varepsilon_y + \varepsilon_z)^2+G\left\{(\varepsilon_x^2 + \varepsilon_y^2 + \varepsilon_z^2)+\frac{1}{2}(\gamma_{xy}^2+\gamma_{yz}^2+\gamma_{zx}^2)\right\}

여기서, ''E'': 영률, ''G'': 전단 탄성 계수, ''ε'': 수직 변형률, ''γ'': 전단 변형률이다. 이 식은 영률이나 푸아송 비에 방향 의존성이 있는 이방성 재료에는 적용할 수 없다.

변형 에너지 함수는 양의 값을 가지므로,

U_0 \ge 0

을 만족하기 위해서는 푸아송 비 ''ν''의 가능한 범위는 다음과 같이 결정된다.^[31]

:

-1 < \nu < 1/2

하한인 −1은 형상 일정(세로 변형률 = 가로 변형률: 즉, 하중 방향에 직각인 방향으로도 늘어남이 생기고, 정육면체의 형상이 유지되는 변화를 나타냄)을 의미한다. 상한인 1/2는 미소 변형률 범위에서 체적 불변을 의미한다.

변형에 따른 체적 변화를 살펴보면 다음과 같다. 세로 방향으로 인장·압축의 단축 하중을 받을 때, 세로 방향의 치수 변화는 (1 + ''ε'') 배가 된다. 한편, 가로 방향의 치수는 (1 − ''νε'') 배가 되며, 단면적 변화는 (1 − ''νε'')² 배가 된다. 따라서 체적 변화는 (1 + ''ε'')(1 − ''νε'')² = (1 - 2''νε'' + ''ε'' − 2''νε''² + ''ν''²''ε''² + ''ν''²''ε''³) 배가 된다. 변형률 ''ε''이 미소 범위라고 하면, ''ε''의 고차항을 무시할 수 있으므로, 체적 변화는 (1 − 2''νε'' + ''ε'') 배가 된다. 이 때, ''ν''가 1/2이면, ''ε''의 값에 관계없이 체적 변화는 항상 1배가 되어 체적 변화 없음·체적 불변이 된다.^[31]

에너지 식에서는 푸아송 비가 음의 값을 가질 수 있지만, 모든 방향에서 영률과 푸아송 비가 같은 등방성 탄성을 가정할 수 있는 재료에서는 푸아송 비가 마이너스가 되는 재료는 존재하지 않는다. 만약 푸아송 비가 마이너스라는 것은, 막대 재료라면 잡아당길수록 두꺼워지는 재료라는 뜻이다. 이방성 재료라면, 방향에 따라 푸아송 비가 마이너스가 될 수 있지만, 전 방향에서 그런 거동을 보이는 것은 아니고, 어디까지나 특정 방향으로 잡아당기면 두꺼워지는 방향이 있을 수 있다는 것이며, 전체 변형 에너지의 균형은 유지된다. 음의 푸아송 비를 나타내는 예로, 실리콘 단결정 등, 대형 단결정 전반이나 크리스토발라이트(SiO₂로 이루어진 결정)가 있다. 또한, 펜타그래핀(오각형의 그래핀)^[33], 내부에 벌집 구조를 가진 재료^[34]에는 방향에 따라 음의 푸아송 비를 나타내는 것이 있지만, 이는 모두 방향에 따라 영률과 푸아송 비가 다른 탄성 이방성을 보이는 재료이며, 등방성 탄성체는 아니다.

4. 2. 이방성 재료

이방성 재료의 경우, 푸아송 비는 잡아당기는 방향과 가로 변형에 따라 달라진다.

:

\begin{align}\nu (\mathbf{n}, \mathbf{m}) &= - E\left(\mathbf n\right) s_{ij \alpha \beta} n_i n_j m_\alpha m_\beta \\[4px]E^{-1} (\mathbf{n}) &= s_{ij\alpha \beta } n_i n_j n_\alpha n_\beta\end{align}

여기서

\nu

는 푸아송 비,

E

는 영률이며,

\mathbf{n}

은 잡아당기는 방향의 단위 벡터,

\mathbf{m}

은 잡아당기는 방향에 수직인 단위 벡터이다. 푸아송 비는 이방성의 유형에 따라 다른 수의 특수 방향을 갖는다.^[11]^[12]

4. 3. 직교 이방성 재료

직교 이방성 재료는 재료 특성에 대해 서로 수직인 세 개의 대칭 평면을 갖는다. 그 예로는 나무가 있는데, 나무는 나뭇결을 따라 가장 강성(및 강도)이 높고 다른 방향으로는 덜하다.^[13]^[14]

후크의 법칙은 행렬 형태로 표현될 수 있다.

:

\begin{bmatrix} \epsilon_{xx} \\ \epsilon_{yy} \\ \epsilon_{zz} \\ 2\epsilon_{yz} \\ 2\epsilon_{zx} \\ 2\epsilon_{xy} \end{bmatrix}= \begin{bmatrix}\tfrac{1}{E_x} & - \tfrac{\nu_{yx}}{E_y} & - \tfrac{\nu_{zx}}{E_z} & 0 & 0 & 0 \\

\tfrac{\nu_{xy}}{E_x} & \tfrac{1}{E_y} & - \tfrac{\nu_{zy}}{E_z} & 0 & 0 & 0 \\
\tfrac{\nu_{xz}}{E_x} & - \tfrac{\nu_{yz}}{E_y} & \tfrac{1}{E_z} & 0 & 0 & 0 \\

0 & 0 & 0 & \tfrac{1}{G_{yz}} & 0 & 0 \\0 & 0 & 0 & 0 & \tfrac{1}{G_{zx}} & 0 \\0 & 0 & 0 & 0 & 0 & \tfrac{1}{G_{xy}} \\\end{bmatrix}\begin{bmatrix}\sigma_{xx} \\ \sigma_{yy} \\ \sigma_{zz} \\ \sigma_{yz} \\ \sigma_{zx} \\ \sigma_{xy}\end{bmatrix}

여기서

''E''_''i''^영어는 축 i^영어를 따른 탄성 계수이다.
''G''_''ij''^영어는 법선이 i^영어 방향인 평면에서 j^영어 방향의 전단 탄성 계수이다.
''ν''_''ij''^영어는 i^영어 방향으로 인장 변형이 가해질 때 j^영어 방향으로의 수축에 해당하는 푸아송 비이다.

직교 이방성 재료의 푸아송 비는 각 방향(x^영어, y^영어 및 z^영어)에서 다르다. 그러나 응력 및 변형률 텐서의 대칭성은 방정식의 여섯 개의 푸아송 비가 모두 독립적인 것은 아님을 의미한다. 독립적인 재료 특성은 탄성 계수 3개, 전단 탄성 계수 3개 및 푸아송 비 3개 등 9개뿐이다. 나머지 3개의 푸아송 비는 다음과 같은 관계식에서 얻을 수 있다.

:

\frac{\nu_{yx}}{E_y} = \frac{\nu_{xy}}{E_x}\,, \qquad\frac{\nu_{zx}}{E_z} = \frac{\nu_{xz}}{E_x}\,, \qquad\frac{\nu_{yz}}{E_y} = \frac{\nu_{zy}}{E_z}

위의 관계식에서 ''E''_''x'' > ''E''_''y''^영어이면 ''ν''_''xy'' > ''ν''_''yx''^영어임을 알 수 있다. 더 큰 비(이 경우 ''ν''_''xy''^영어)는 '''주요 푸아송 비'''라고 하고 더 작은 비(이 경우 ''ν''_''yx''^영어)는 '''부 푸아송 비'''라고 한다. 다른 푸아송 비 사이에서도 유사한 관계를 찾을 수 있다.

4. 4. 횡등방성 재료

횡등방성 재료는 탄성 특성이 등방성인 등방성 평면을 갖는다. 이 등방성 평면이 yz|yz^영어 평면이라고 가정하면, 훅의 법칙은 다음과 같은 형식을 취한다.^[15]

상수 수를 줄이기 위해 yz|yz^영어 등방성 평면을 사용했다. 즉,

:

E_y = E_z,\qquad \nu_{xy} = \nu_{xz},\qquad \nu_{yx} = \nu_{zx} .

.

응력 텐서와 변형률 텐서의 대칭성은 다음을 의미한다.

:

\frac{\nu_{xy}}{E_x} = \frac{\nu_{yx}}{E_y} ,\qquad \nu_{yz} = \nu_{zy} .

이로 인해 ''E''_''x'', ''E''_''y'', ''G''_''xy'', ''G''_''yz'', ''ν''_''xy'', ''ν''_''yz''의 6개의 독립적인 상수가 남는다. 그러나 횡등방성은 ''G''_''yz''와 ''E''_''y'', ''ν''_''yz'' 사이의 추가 제약 조건을 발생시킨다.

:

G_{yz} = \frac{E_y}{2\left(1+\nu_{yz}\right)} .

따라서 두 개가 푸아송 비인 5개의 독립적인 탄성 재료 특성이 있다. 가정된 대칭 평면의 경우, ''ν''_''xy''와 ''ν''_''yx'' 중 더 큰 값이 주 푸아송 비이다. 다른 주 및 종 푸아송 비는 같다.

5. 다양한 재료의 푸아송 비 값

재료	푸아송 비	출처
고무	0.4999^[17]
금	0.42–0.44
포화된 점토	0.40–0.49
마그네슘	0.252–0.289
티타늄	0.265–0.34
구리	0.33
알루미늄 합금	0.32
점토	0.30–0.45
스테인리스강	0.30–0.31
강철	0.27–0.30
주철	0.21–0.26
모래	0.20–0.455
콘크리트	0.1–0.2
유리	0.18–0.3
금속 유리	0.276–0.409^[18]
폼	0.10–0.50
코르크	0.0

재료	대칭면
노멕스 복합체 허니컴 허니컴 코어	, 리본은 방향	0.49	0.69	0.01	2.75	3.88	0.01
유리 섬유 에폭시 수지		0.29	0.32	0.06	0.06	0.32

재료	푸아송 비	출처
천연 고무	0.49	^[35]
고밀도 폴리에틸렌	0.30	^[31]
폴리스티렌	0.35	^[31]
폴리카보네이트	0.39	^[31]
폴리아세탈	0.32	^[31]
에폭시 수지	0.37	^[31]
텅스텐	0.28	^[36]
알루미늄	0.345	^[37]
몰리브덴	0.31	^[38]
유리	0.27	^[31]
구리	0.343	^[31]
주철	0.27	^[31]
강	0.28 - 0.30	^[31]
황동 (아연 30%)	0.35	^[31]
납	0.44	^[31]
금	0.44	^[31]
주석	0.36	^[39]
탄탈	0.35	^[40]
니오브	0.35	^[41]
크롬	0.21	^[42]
사암	0.14 - 0.33	^[31]
안산암	0.07 - 0.22	^[31]
결정 편암	0.08 - 0.20	^[31]
석회암	0.19 - 0.27	^[31]
대리석	0.25 - 0.38	^[31]
화강암	0.25 - 0.38	^[31]
다이아몬드	0.2	^[31]
코르크	거의 0	^[31]

5. 1. 음의 푸아송 비 재료

오세틱 재료라고 불리는 일부 재료는 음의 푸아송 비를 갖는 특이한 성질을 보인다. 이러한 재료는 한 방향으로 늘어나면 수직 방향으로도 두꺼워지는, 즉 팽창하는 경향을 보인다. 이는 일반적인 재료가 늘어날 때 수직 방향으로 수축하는 것과는 반대되는 현상이다.

이러한 음의 푸아송 비는 주로 독특하게 배향된 경첩 형태의 분자 결합 구조 때문에 발생한다. 이러한 구조에서 종축 방향으로 힘을 가해 늘리면, 경첩이 횡 방향으로 '열리는' 효과가 발생하여 단면적이 증가하고, 결과적으로 양의 횡 방향 변형률을 나타낸다.^[19]

음의 푸아송 비를 갖는 재료는 구조적으로 설계될 수 있으며, 이는 기계적 메타물질과 같은 새로운 재료 설계 분야로 이어지고 있다. 연구에 따르면 특정 종류의 목재는 압축 크리프 시험에서만 음의 푸아송 비를 나타내기도 한다.^[20]^[21] 초기에는 양의 푸아송 비를 보이다가 시간이 지남에 따라 점차 감소하여 음의 값을 갖게 되는데, 이는 목재의 푸아송 비가 시간에 따라 변하며, 축 방향과 횡 방향 변형률이 동일한 속도로 증가하지 않음을 의미한다.

엔지니어링된 미세 구조를 가진 매체 또한 음의 푸아송 비를 나타낼 수 있다. 예를 들어, 재료를 제거하고 주기적인 다공성 매체를 생성하면 부압성을 얻을 수 있다.^[22] 격자 구조는 푸아송 비의 낮은 값에 도달하게 할 수 있으며,^[23] 등방성 재료의 경우 -1에 가까운 값을 갖도록 설계할 수도 있다.^[24]

300개 이상의 결정성 물질이 음의 푸아송 비를 갖는 것으로 알려져 있다.^[25]^[26]^[27] 여기에는 Li, Na, K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn, Sr, Sb, MoS₂ 등이 포함된다.

하지만, 모든 방향에서 영률과 푸아송 비가 같은 등방성 탄성 재료에서는 푸아송 비가 음수가 될 수 없다. 이방성 재료의 경우 특정 방향에서 음의 푸아송 비를 가질 수 있지만, 이는 특정 방향으로 잡아당겼을 때 두꺼워지는 방향이 있다는 것을 의미하며, 전체적인 변형 에너지의 균형은 유지된다. 음의 푸아송 비를 나타내는 예로는 실리콘 단결정, 크리스토발라이트(SiO₂) 결정, 펜타그래핀(그래핀)^[33], 벌집 구조를 가진 재료^[34] 등이 있지만, 이들은 모두 방향에 따라 영률과 푸아송 비가 다른 탄성 이방성을 보이는 재료들이다.

6. 푸아송 함수

유한 변형 이론에서 가로 변형률과 세로 변형률 간의 관계는 일반적으로 푸아송 비로 잘 설명되지 않는다. 푸아송 비는 큰 변형 영역에서 적용된 변형률의 함수로 간주되는 경우가 많다. 이러한 경우, 푸아송 비는 푸아송 함수로 대체되며, 여기에는 헹키(Hencky), 비오(Biot), 그린(Green), 알망시(Almansi) 함수 등 여러 정의가 있다.^[28] 가로 신장 λ|람다^영어_trans = ε_trans + 1 및 세로 신장 λ|람다^영어_axial = ε_axial + 1을 정의할 때, 가로 신장은 세로 신장의 함수이며, 가장 일반적인 함수는 다음과 같다.

헹키(Hencky) 함수

: ν|뉴^영어^Hencky = -{{ln λ_trans}ln λ_axial}

비오(Biot) 함수

: 뉴/ν^영어^Biot =

그린(Green) 함수

: 뉴/ν^영어^Green =

알망시(Almansi) 함수

: 뉴/ν^영어^Almansi =

7. 푸아송 효과의 응용

푸아송 효과는 가압 파이프 흐름, 구조 지질학, 코르크 마개, 자동차 정비 등 다양한 분야에서 중요한 영향을 미친다. 가압 파이프 흐름에서 푸아송 효과는 파이프 연결부 변형 및 파손의 원인이 될 수 있다. 구조 지질학에서는 암석의 변형과 균열 형성에 영향을 미치며, 코르크 마개는 푸아송 비가 0이어서 와인 병 마개로 적합하다. 자동차 정비 시 고무 호스를 분리하기 어려운 현상도 푸아송 효과로 설명된다.

7. 1. 가압 파이프 흐름

푸아송 효과가 뚜렷하게 나타나는 분야 중 하나는 가압 파이프 흐름이다. 파이프 내부의 공기나 액체가 고압 상태가 되면 파이프 내부에 균일한 힘이 작용하여 파이프 재료에 후프 응력을 발생시킨다. 이러한 후프 응력은 푸아송 효과로 인해 파이프 직경을 늘리고 길이는 약간 줄어들게 한다. 특히 길이 감소는 파이프 연결부에 큰 영향을 줄 수 있는데, 이는 각 파이프 부분이 연속적으로 연결되어 효과가 누적되기 때문이다. 이로 인해 연결부가 분리되거나 파손될 위험이 커진다.

7. 2. 구조 지질학

대부분의 재료와 마찬가지로 암석은 응력을 받으면 푸아송 효과의 영향을 받는다. 지질학적 시간 척도에서 지구 지각의 과도한 침식 또는 퇴적은 기반암에 큰 수직 응력을 생성하거나 제거할 수 있다. 이 암석은 가해진 응력의 직접적인 결과로 수직 방향으로 팽창하거나 수축하며, 푸아송 효과의 결과로 수평 방향으로 변형되기도 한다. 수평 방향의 이러한 변형 변화는 암석에 균열과 잠재 응력에 영향을 미치거나 균열을 형성할 수 있다.^[29]

7. 3. 코르크 마개

코르크는 불활성, 불침투성, 유연성, 밀봉성, 탄성 등 여러 이유로 역사적으로 와인 병을 봉하는 데에 선택되었지만,^[30] 푸아송 비가 0이라는 점도 또 다른 장점을 제공한다. 코르크가 병에 삽입될 때 윗부분은 축 방향으로 압축되어도 직경이 팽창하지 않는다. 코르크를 병에 삽입하는 데 필요한 힘은 코르크와 병 사이의 마찰에서만 발생한다. 만약 마개가 고무로 만들어진 경우(푸아송 비가 약 +0.5) 고무 마개 윗부분이 반경 방향으로 팽창하는 것을 극복하기 위해 비교적 큰 추가 힘이 필요하게 된다.

7. 4. 자동차 정비

대부분의 자동차 정비공은 고무 호스(예: 냉각수 호스)를 금속 파이프 스터브에서 빼내기 어렵다는 것을 알고 있다. 이는 당기는 힘이 호스의 직경을 줄여 스터브를 단단히 잡기 때문이다. (이것은 중국식 손가락 덫에서 나타나는 것과 같은 효과이다.) 호스는 넓고 평평한 칼날을 사용하여 스터브에서 밀어내는 것이 더 쉽다.

참조

_[1] 서적 Nature and Properties of Engineering Materials John Wiley & Sons, Inc
_[2] 학술지 Negative compressibility, negative Poisson's ratio, and stability 2008
_[3] 학술지 Poisson's ratio values for rocks 2007-01
_[4] 서적 Seismic Performance of Steel-Encased Concrete Piles
_[5] 웹사이트 Folded Shell Structures, PhD Thesis http://www.markschen[...] University of Cambridge, Clare College
_[6] 학술지 Geometric Mechanics of Periodic Pleated Origami https://www.seas.har[...] 2013-05-21
_[7] 학술지 Unraveling metamaterial properties in zigzag-base folded sheets 2015
_[8] 학술지 Zigzag-base folded sheet cellular mechanical metamaterials
_[9] 학술지 Hierarchical honeycomb auxetic metamaterials 2015-12-16
_[10] 학술지 Limits to Poisson's ratio in isotropic materials—general result for arbitrary deformation Chemistry Division, Naval Research Laboratory 2012-04-03
_[11] 학술지 Extreme values of Poisson's ratio of cubic crystals 2016
_[12] 학술지 Extreme values of Young's modulus and Poisson's ratio of hexagonal crystals 2019
_[13] 서적 Advanced Mechanics of Materials Wiley 1993
_[14] 서적 Theory of elasticity of an anisotropic elastic body https://archive.org/[...] Mir Publishing
_[15] 서적 Stress Concentrations in Laminated Composites Technomic Publishing Company 1994
_[16] 웹사이트 Poisson's Ratio Calculation for Glasses http://www.glassprop[...] 2018-04-28
_[17] 학술지 Limits to Poisson's ratio in isotropic materials http://polymerphysic[...] 2014-09-24
_[18] 학술지 Journal of Applied Physics 110, 053521 (2011)
_[19] 웹사이트 Negative Poisson's ratio http://silver.neep.w[...] 2018-04-28
_[20] 학술지 Viscoelastic characterization of wood: Time dependence of the orthotropic compliance in tension and compression 2013-03
_[21] 학술지 Time dependence of the orthotropic compression Young's moduli and Poisson's ratios of Chinese fir wood http://doc.rero.ch/r[...] 2016-11-01
_[22] 학술지 Design of a porous material with isotropic negative Poisson's ratio 2016
_[23] 학술지 A class of auxetic three-dimensional lattices https://id.elsevier.[...] 2016
_[24] 학술지 Auxetic two-dimensional lattices with Poisson's ratio arbitrarily close to -1 2014
_[25] 학술지 Classification of cubic auxetics 2013
_[26] 학술지 Variability of elastic properties of hexagonal auxetics 2011
_[27] 학술지 Auxetics among 6-constant tetragonal crystals 2015
_[28] 학술지 How to characterize a nonlinear elastic material? A review on nonlinear constitutive parameters in isotropic finite elasticity 2017-11-03
_[29] 웹사이트 Lecture Notes in Structural Geology – Effective Stress http://www3.geosc.ps[...] 2019-07-03
_[30] 웹사이트 Cork: properties, capabilities and applications https://thematking.c[...] 2017-05-04
_[31] 서적 機械工学辞典丸善 2007-01-20
_[32] 백과사전 Poisson effect http://www.oxfordref[...] 2014-04-26
_[33] 뉴스 五角形のグラフェンの発見-夢の新素材として期待- http://www.tohoku.ac[...] 東北大学
_[34] 웹사이트 Negative Poisson's ratio materials http://silver.neep.w[...] 2014-01-02
_[35] 서적 工学技術者の高分子材料入門共立出版 2003-10-01
_[36] 웹사이트 材料紹介：タングステン http://www.plansee.c[...] プランゼージャパン 2014-03-09
_[37] 서적 物理学裳華房
_[38] 웹사이트 材料紹介：モリブデン http://www.plansee.c[...] プランゼージャパン 2014-03-09
_[39] 서적 材料強度学コロナ社 2011-05-02
_[40] 웹사이트 材料紹介：タンタル http://www.plansee.c[...] プランゼージャパン 2014-03-09
_[41] 웹사이트 材料紹介：ニオブ http://www.plansee.c[...] プランゼージャパン 2014-03-09
_[42] 웹사이트 材料紹介：クロム http://www.plansee.c[...] プランゼージャパン 2014-03-09

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com